Padding Oracle Attack(Shiro-721)漏洞复现
漏洞概述
由于Shiro cookie中通过AES/CBC/PKCS5加密rememberMe字段,攻击者可以控制rememberMe字段的前16字节(IV),通过Padding Oracle攻击来构造恶意的rememberMe字段,进行反序列化攻击,最终导致任意代码执行。
影响版本
Apache Shiro <1.42
漏洞原理
Shiro-721漏洞是因为使用AES/CBC/PKCS5导致了Padding Oracle 攻击,下面详细介绍Padding Oracle Attack(填充提示攻击)
Padding Oracle Attack
该漏洞存在条件如下:
- 攻击者获取密文,IV(初始向量,rememberMe字段的前16字节)。
- 修改密文并且触发解密操作,解密成功和解密失败存在差异性。
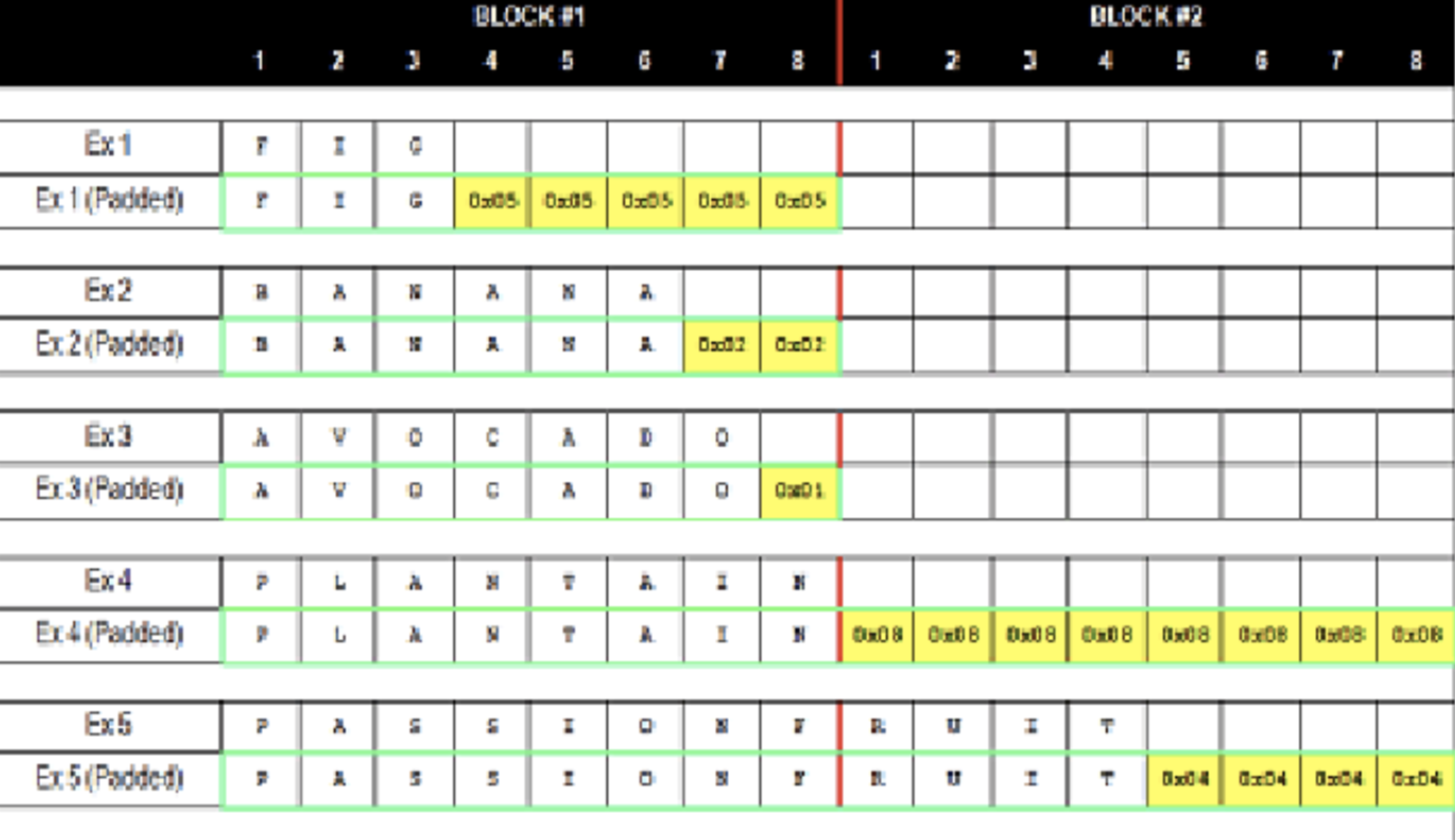
1. 分组密码的填充
AES、DES在加密时一般会采用分组加密,将明文进行分组,常见的64bit、128bit、256bit。
分组带来一个问题,就是明文不可能恰好是block的整数倍,对于不能整除剩余的部分数据就涉及到填充操作。
常用的填充操作有PKCS5和PKCS7,在最后一个block中将不足的bit位数作为bit值进行填充,例如最后一个分组(block)缺少3个bit,就填充3个0x03到结尾,缺少n个bit,就填充n个0x0n。在解密时会校验明文的填充是否满足该规则,如果是以N个0x0N结束,则意味着解密操作执行成功,否则解密操作失败。
2. CBC模式密码算法
分组密码算法有四种模式,分别是ECB、CBC、CFB和OFB,其中CBC是IPSEC的标准做法,CBC主要是引入一个初始化向量(IV)来加强密文的随机性,保证相同明文通过相同的密钥加密的结果不一样。
CBC加密过程:
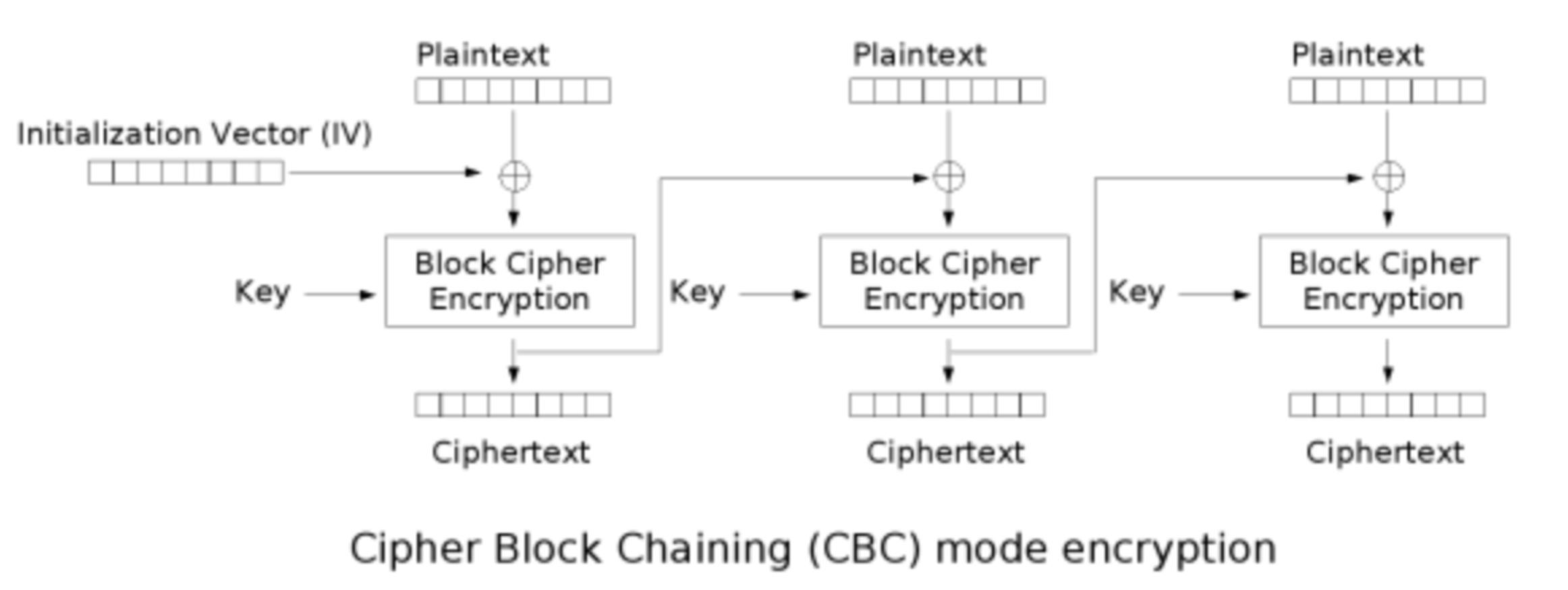
- 明文经过填充后,分为不同的组block,以组的方式对数据进行处理
- 初始化向量(IV)首先和第一组明文进行XOR(异或)操作,得到”中间值“
- 采用密钥对中间值进行块加密,删除第一组加密的密文 (加密过程涉及复杂的变换、移位等)
- 第一组加密的密文作为第二组的初始向量(IV),参与第二组明文的异或操作
- 依次执行块加密,最后将每一块的密文拼接成密文
由于初始化向量(IV)每次加密都是随机的,所以IV经常会被放在密文的前面,解密时先获取前面的IV,再对后面的密文进行解密
CBC解密过程:
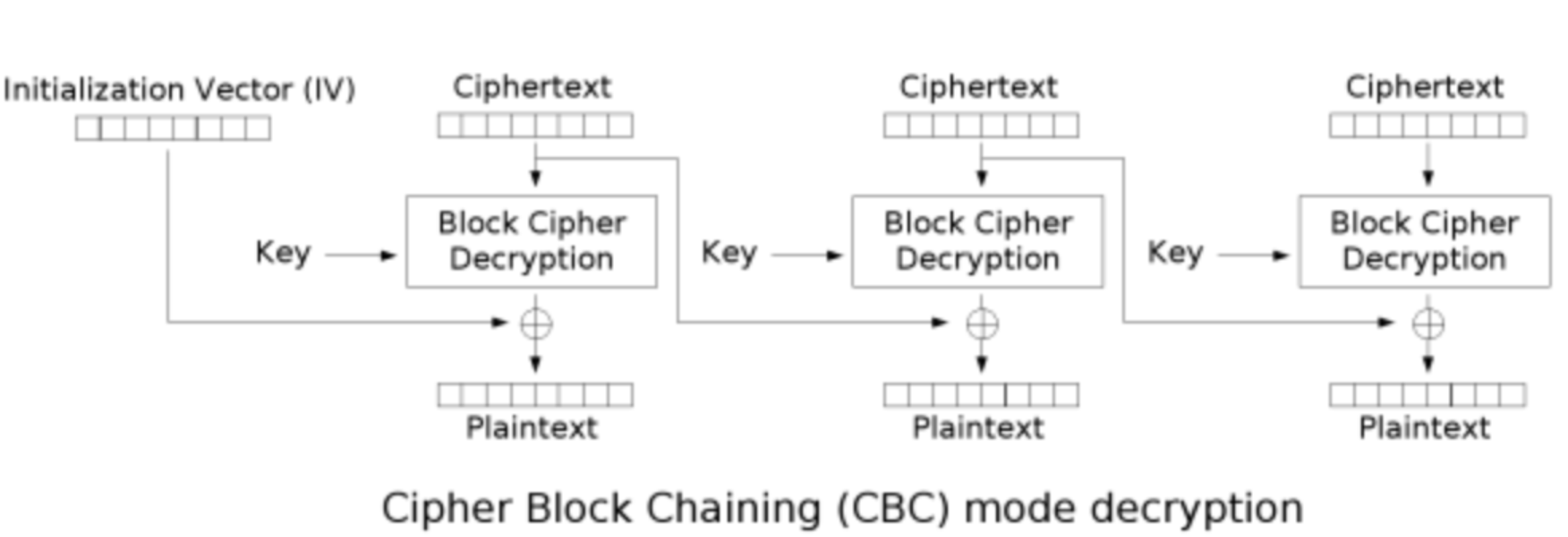
- 会将密文进行分组(按照加密采用的分组大小),前面的第一组是初始化向量,从第二组开始才是真正的密文
- 使用加密密钥对密文的第一组进行解密,得到”中间值“
- 将中间值和初始化向量进行异或,得到该组的明文
- 前一块密文是后一块密文的IV,通过异或中间值,得到明文
- 块全部解密完成后,拼接得到明文,密码算法校验明文的格式(填充格式是否正确)
- 校验通过得到明文,校验失败得到密文
3. padding oracle attack破解密文的明文
此处以一个例子进行猜解,假设有这样一个应用,请求如下:
1 | |
现在让我们来看看在不知道明文的情况下,如何猜解处明文。首先我们将密文分组,前面8个字节为初始化向量,后面16个字节为加密后的数据:
1 | |
首先我们破解第一组密文http://www.example.com/decrypt.jsp?data=7B216A634951170FF851D6CC68FC9537通过构造前面初始向量即可破解出第一组密文的明文
将初始化向量全部设置为0,提交如下请求
http://www.example.com/decrypt.jsp?data=00000000000000000F851D6CC68FC9537,服务器势必会解密失败,返回HTTP 500,那是因为在对数据进行解密的时候,明文最后一个字节的填充是Ox3D,不满足填充规则,校验失败,此时示意图如下: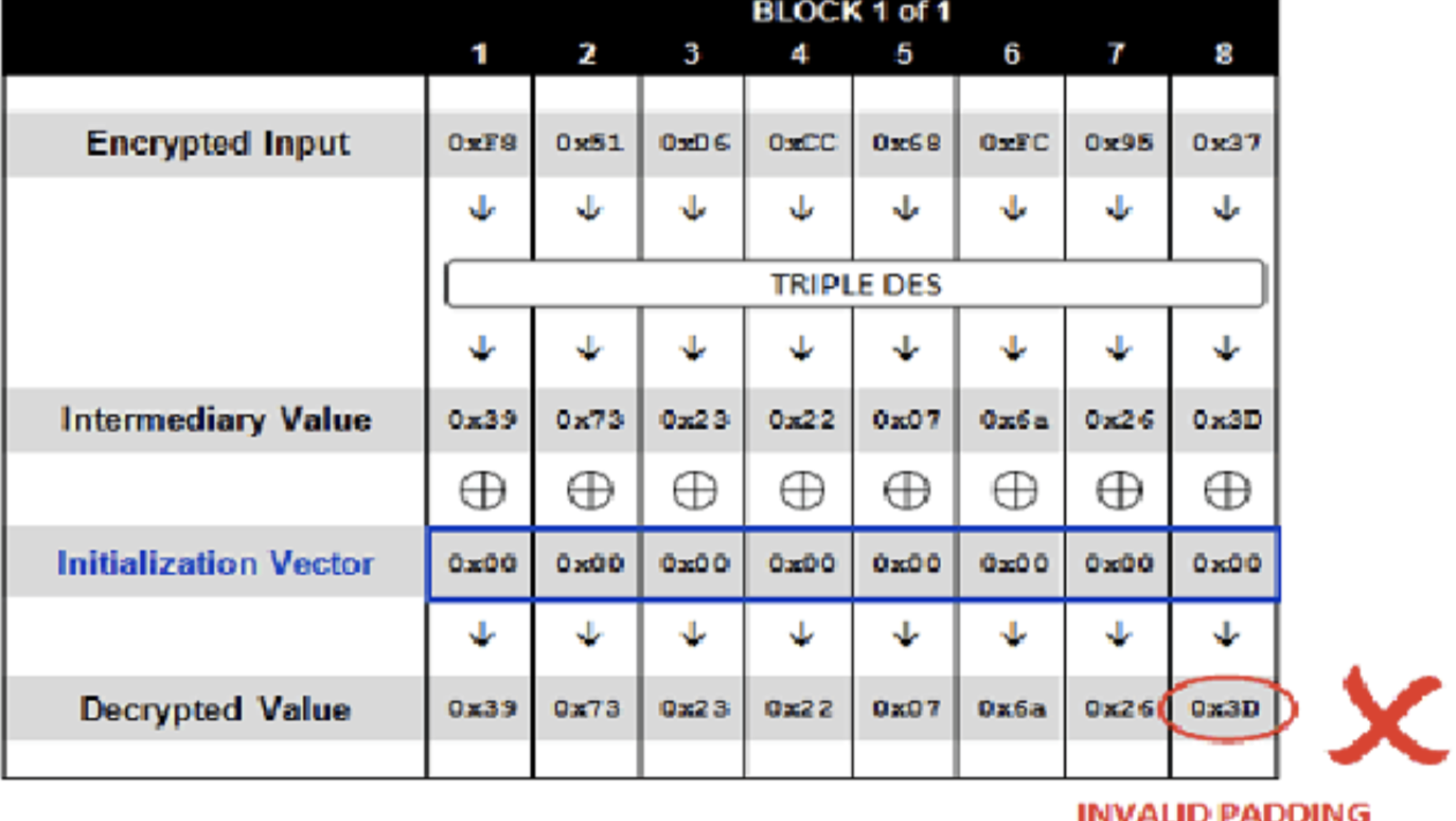
依次将初始化向量最后一个字节从0x01~0xFF递增,直到解密的明文最后一个字节为0x01,成为一个正确的padding,当初始化向量为
000000000000003C时,成功了,服务器返回HTTP 200,解密示意图如下: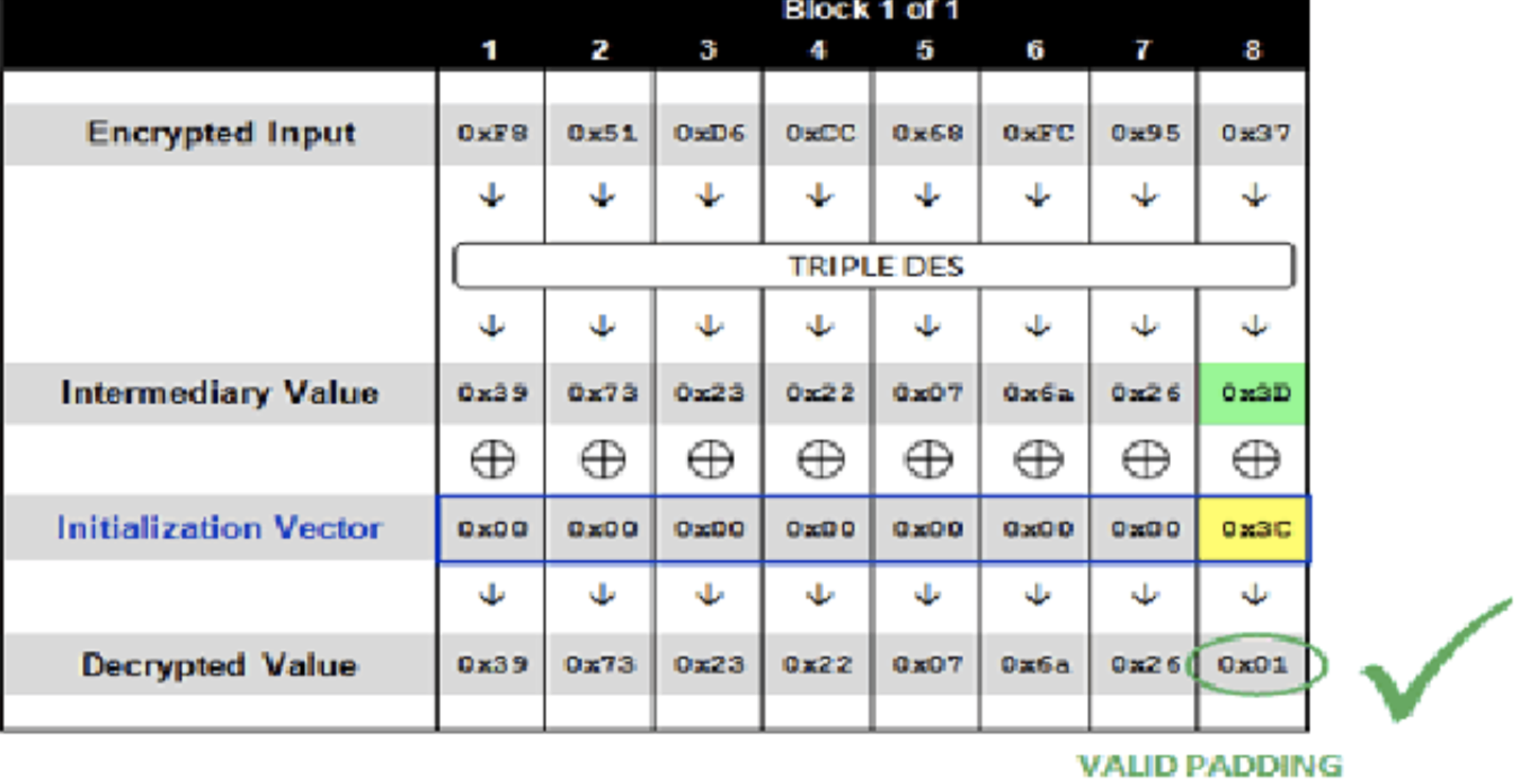
我们已知构造成功的IV最后一个字节为0x3C,最后一个填充字符为0x01,则我们能通过异或XOR计算出,第一组密文解密后的中间值最后一个字节:0x01 xor 0x3C = 0x3D;
重点:第一组密文解密的中间值是一直不变的,同样也是正确的,我们通过构造IV值,使得最后一位填充值满足0x01,符合padding规则,则意味着程序解密成功(当前解密的结果肯定不是原来的明文),通过循环测试的方法,猜解出中间值得最后一位,再利用同样的方式猜解前面的中间值,直到获取到完整的中间值下面我们将构造填充值为0x02 0x02的场景,即存在2个填充字节,填充值为0x02,此时我们已经知道了中间值得最后一位为0x3D,计算出初始向量的最后一位为 0x3D xor 0x02 = 0x3F, 即初始向量为
0000000000000003F,遍历倒数第二个字节从0x00~0xFF,直到响应成功,示例图如下:
此时,我们猜解出中间值得后两个字节分别为 0x26 0x3D
通过同样的方式,完成第一组密文中间值得猜解
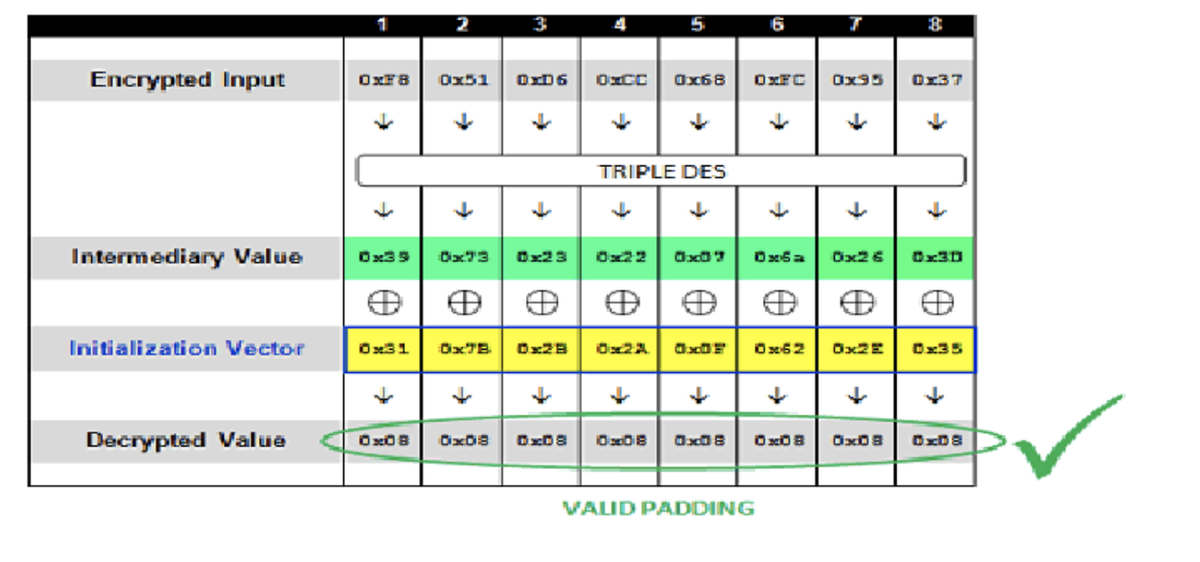
当第一组密文的中间值猜解成功后,我们将中间值和已知的IV做异或,则得到第一组密文的明文
1
2
3
4
50x39 0x73 0x23 0x22 0x07 0x6A 0x26 0x3D
xor
0x7B 0x21 0x6A 0x63 0x49 0x51 0x17 0x0F
=
BRIAN;12继续破解第二组密文,第二组密文的IV向量是第一组密文,随意按照上述的逻辑构造第一组密文,即可破解出第二组明文。
4. 伪造明文的密文
在不知道密钥的情况下,完成数据的加密,绕过服务端的校验(解密成功+明文有效),达到攻击的目的;
伪造明文其实就是上面猜解逆向的过程。通过遍历密文+已知的IV+Padding来确定伪造的密文。
漏洞修复
- 更新版本Apache Shior到最新版本
- 关闭rememberMe持久化登录功能
- 临时防范建议:
- 拦截Cookie中长度过大的rememberMe值
- 拦截访问过于频繁的IP, 因为该漏洞需要爆破Cookie
官方修复方案
在>=1.4.2版本中,官方对Shiro-721漏洞做了修复。
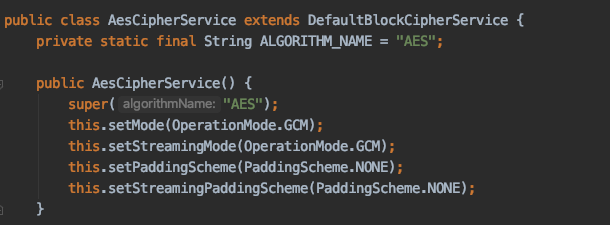
1.4.1 版本(有漏洞版本)
AesCipherService类中设置使用的加密算法
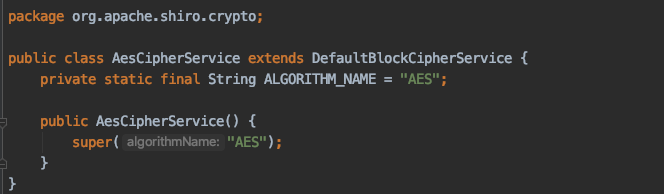
设置加密算法采用AES,其父类AbstractSymmetricCipherService指定了加密模式及填充方式为CBC/PKCS5
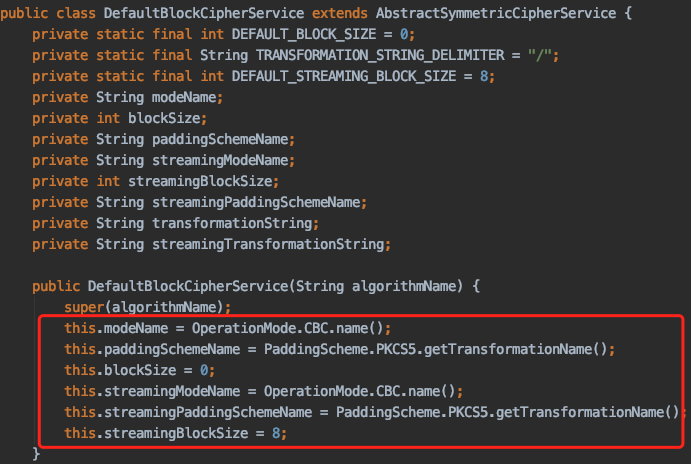
1.4.2 版本(修复版本)
AesCipherService类,加密方式由CBC更换为GCM

1.8.0 版本(2021-8-24版本)
AesCipherService类,加密方式为GCM并设置填充方式为NoPadding
CBC与GCM加密模式区别
AES/GCM是流加密的模式,不需要对明文进行填充。AES/CBC是块加密的模式,需要对明文进行填充。
AES/CBC中必须要用到padding,导致最后一个明文块与其他密文块不同,因此可能会受到padding Oracle attacks,从而可以直接通过初始向量IV和密码,即可得到明文。
AES/GCM可以并行加密解密,AES/CBC的模式决定了它只能串行地进行加密。因为加密是耗时较久的步骤。
AES/GCM提供了GMAC信息校验码,用以校验密文的完整性。AES/CBC没有,无法有效地校验密文的完整性。
AES/GCM中进行AES加密的是counter,AES/CBC中进行AES加密的是明文块。
GCM(GMAC Counter Mode),使用了Counter的模式,并且带有GMAC消息认证码,因为GCM是基于CTR(Counter Mode)的,所以以下介绍CTR Mode:
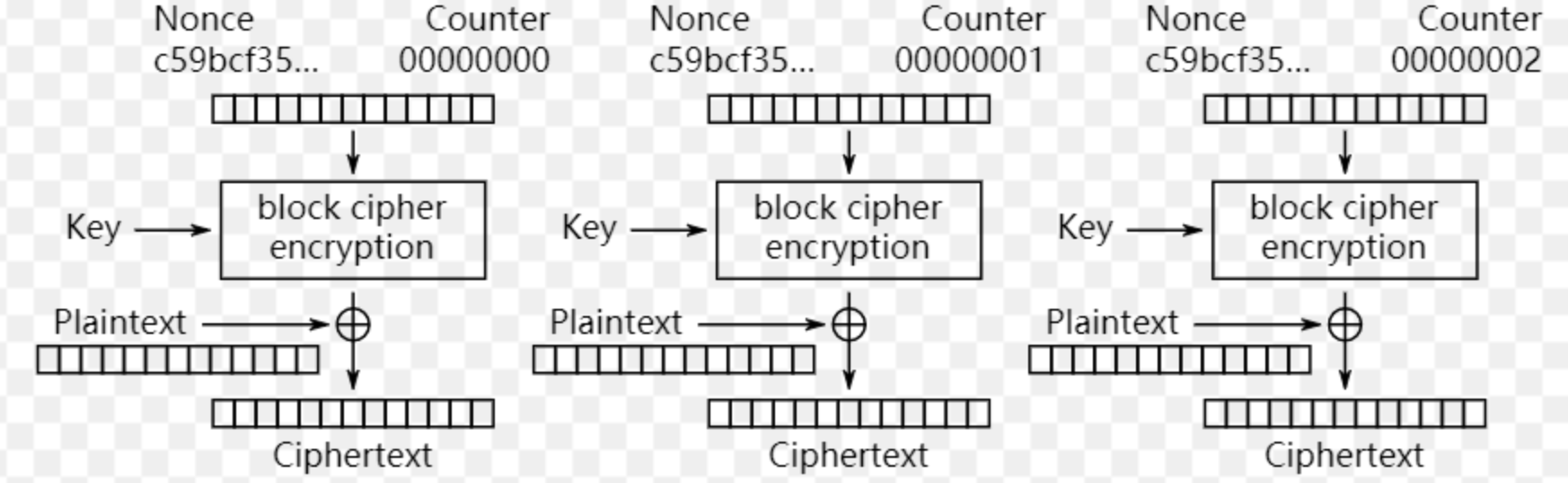
从上图可知,在CTR模式中,不再对明文进行加密,而是对一个逐次累加的计数器进行加密,用加密后得到的比特序列与明文分组进行异或,得到每一个明文块的密文。计数器的初始值,是依据于一个nonce的。
因为计数器是递增的,所以加密得到的比特序列是不同的,再与明文进行异或,可以避免相同的明文块被加密成一样的密文块。
因为每一个明文块的加密都是独立的,不依赖于其他明文块,所以CTR模式的AES加密是可以并行地对明文块进行加密的,并且不会有错误传播的现象。
以下为CTR解密模式:
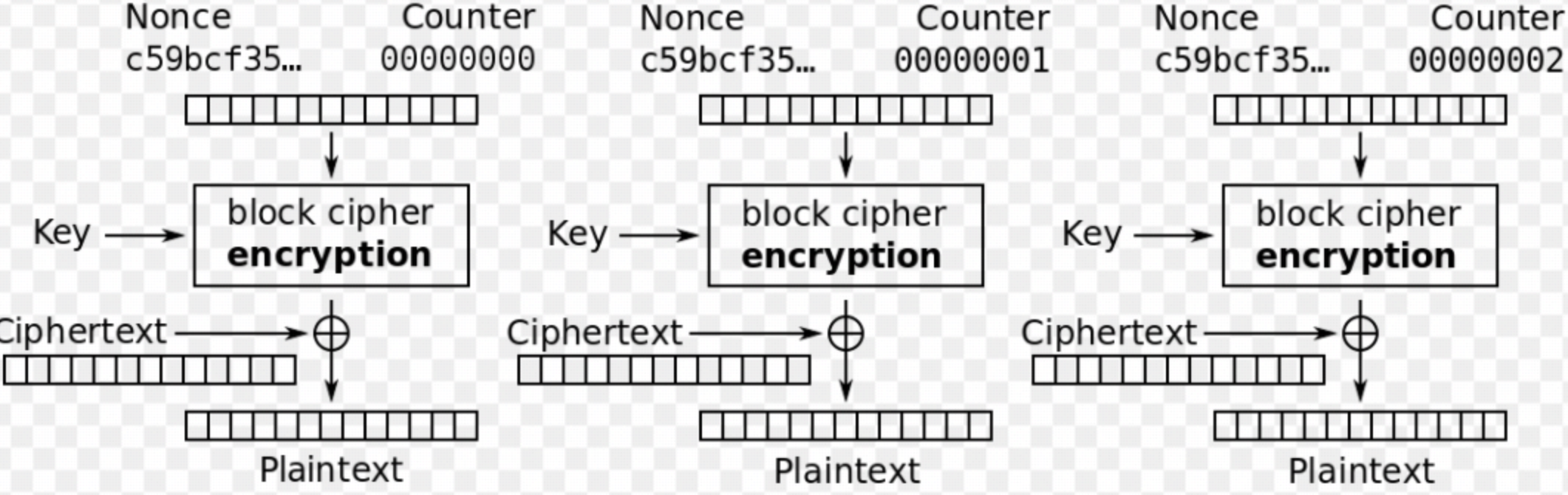
CTR的解密也是较为直接的。直接对计数器进行加密,得到比特序列,再和对应的密文块进行异或,就可以得到相应的明文块。
因为CTR模式下的AES加密是针对计数器进行加密的,所以CTR模式是不需要padding的。